複素電磁界同士の減算により、合成波を構成する複数の波に分離できます。入射波と反射波で生成される合成波を考えると、合成波の複素電界は以下の式で表されます。

また、以下の式が成り立ちます。

合成波の複素電界を入射波と反射波に分離します。

したがって、各点おける合成波が作る複素電界から入射波だけが作る複素電界を差し引けば、反射波の複素電界が抽出できます。合成波の磁界も同様に入射波成分と反射成分に分離し、Fig 8で図示された“電磁波エネルギーの流れ”を表すポインティングベクトル

を算出することで、透過率や反射率を求めることができます。
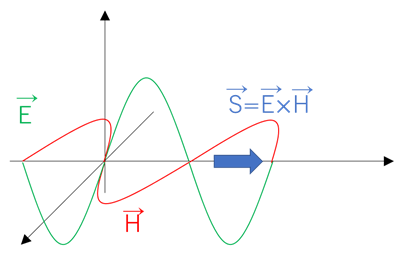
Fig 8 ポインティングベクトルSとE, Hの関係
以下では、真空中に置かれた屈折率n=3の物体に対する反射率と透過率を、複素電磁界から求めます。Fig 9が示すように、物体の反射による合成波が生成されるtargetモデルと、励振源からの電磁波がそのまま伝送するblankモデルを用意します。targetモデルとblankモデルの積算電磁界分布を複素数で出力し、その差分を計算することで反射波成分を抽出できます。

Fig 9 n=3の物体を有するtargetモデル(左)とblankモデル(右)
矩形励振源はtargetモデル・blankモデルの解析領域内で同位置にあり、電界Eはy方向、磁界Hはx方向に振動しています。ポインティングベクトルSはz方向に進行します。このモデルでは、電磁波のx, y方向への散乱がないため、電磁波エネルギーはz方向のみを考慮すれば十分です。そこで、x-y断面の中心点を貫くz軸上の各点におけるReEy, ImEy, ReHx, ImHx, Szに着目します。
以下に二つのモデルから得られたSzについての積算結果を示します。Fig 10はtargetモデル、Fig 11はblankモデルのSz分布です。

Fig 10 targetモデルのSz分布

Fig 11 blankモデルのSz分布
どちらもz=2400 nmに位置する矩形励振源を境にSzが逆転し、Fig 11のblankモデルではその絶対値が等しいことが確認できます。また、Fig 10のtargetモデルについて、物体と励振源の間の領域(z=1200nm-2400nm)では入射波と反射波が逆向きから合成され、励振源の向こう側(z=2400nm-3600nm)では入射波と反射波が同じ向きで合成されています。

また、以下の式が成り立ちます。

合成波の複素電界を入射波と反射波に分離します。

したがって、各点おける合成波が作る複素電界から入射波だけが作る複素電界を差し引けば、反射波の複素電界が抽出できます。合成波の磁界も同様に入射波成分と反射成分に分離し、Fig 8で図示された“電磁波エネルギーの流れ”を表すポインティングベクトル


以下では、真空中に置かれた屈折率n=3の物体に対する反射率と透過率を、複素電磁界から求めます。Fig 9が示すように、物体の反射による合成波が生成されるtargetモデルと、励振源からの電磁波がそのまま伝送するblankモデルを用意します。targetモデルとblankモデルの積算電磁界分布を複素数で出力し、その差分を計算することで反射波成分を抽出できます。

矩形励振源はtargetモデル・blankモデルの解析領域内で同位置にあり、電界Eはy方向、磁界Hはx方向に振動しています。ポインティングベクトルSはz方向に進行します。このモデルでは、電磁波のx, y方向への散乱がないため、電磁波エネルギーはz方向のみを考慮すれば十分です。そこで、x-y断面の中心点を貫くz軸上の各点におけるReEy, ImEy, ReHx, ImHx, Szに着目します。
以下に二つのモデルから得られたSzについての積算結果を示します。Fig 10はtargetモデル、Fig 11はblankモデルのSz分布です。


どちらもz=2400 nmに位置する矩形励振源を境にSzが逆転し、Fig 11のblankモデルではその絶対値が等しいことが確認できます。また、Fig 10のtargetモデルについて、物体と励振源の間の領域(z=1200nm-2400nm)では入射波と反射波が逆向きから合成され、励振源の向こう側(z=2400nm-3600nm)では入射波と反射波が同じ向きで合成されています。
合成波の分離により反射率を算出する前に、透過率を求めてみます。透過波は入射波と同位相になり、このモデルにある物体は等方性媒質なので、透過波のポインティングベクトル: Sz_target(z=0-1200nm)は一定値をとります。ここで透過率Tを

とすると、T≒0.75となり、フレネルの法則

から得られる理論値: T=0.75と一致します。
次に、合成波から反射波成分を抽出し、反射率を算出します。targetモデルでの積算結果の複素電磁界からblankモデルでの積算結果の複素電磁界を減算し、

を得ます。複素磁界のx成分: Hx*も同様に差分を計算し、反射波のポインティングベクトルのz成分: Re[Sz*_reflected]を、以下のように求めます。※今回のモデルでは、電磁界の散乱がほぼ無視できるので、Ex*_reflected=0, Hy*_reflected=0です。

Re[Sz*_reflected]の分布をFig 12に示します。

物体からの反射波の電磁波エネルギーが、z=1200-3600nmの領域で一定値をとることが確認できました。 さらに、Re[Sz*_reflected]=Sz_reflectedとし、反射率Rを以下の式から求めます。

R=0.23となり、フレネルの法則

以上の計算から、複素電磁界から電磁波の分離を行い、透過波や反射波が計算可能であることが示されました。定在波法(VSWR法)などで反射率を求めるのが適当でないケースで有効な手法だと考えられます。
積算結果ファイル .btecを用いた具体的な手順は、以下のページに記載しています。
https://help.kagiken.co.jp/articles/complex-electromagnetic-field-demultiplexing-procedure