複素振幅は、電界分布及び磁界分布の振幅と位相情報を複素数形式で表したものです。複素電界、複素磁界とも呼称します。複数の電磁波解析結果の加算、減算が可能なことが特徴です。
或る位置の複素振幅は、『定常状態で1周期電磁波解析し、その位置での正弦波形の振幅及び位相を複素数で表した数値』です。定常状態では、Fig 1で示すように、解析領域内全ての位置で電磁界が正弦波形になるので複素電界及び複素磁界の分布が得られます。

Fig 1 ある点における時系列の電界強度(一定時間経過後には定常状態になる)
波の基本式で電界を表示します。

A: 振幅、k: 波数、ω:各周波数、φ:初期位相
θ=kr-ωt-Φとすると、

となり、オイラー公式 を用いると E = Re[Aexp(iθ)]なので、Eを複素数表示すると、


波の基本式で電界を表示します。

θ=kr-ωt-Φとすると、

となり、オイラー公式 を用いると E = Re[Aexp(iθ)]なので、Eを複素数表示すると、

となります。また、振幅Aと位相θは以下の式で表されます。


単純な平面波を伝送した場合の複素電界がどうなるか見てみます。Fig 2 は、真空中をx-y平面に無限に広い矩形励振源(電界はy方向、磁界はx方向に振動)から±z方向に電磁波が伝送している、というモデルを解析した時の複素電界E*のy成分を示しています。橙色点線は矩形励振源の位置を指しています。

Re[E*], Im[E*]は、位相θに対しそれぞれsinθ, cosθから算出しているため、Re[E*]がIm[E*]よりπ/4だけ進んだ波形が得られています。
Fig 3は、Re[Ey*]とIm[Ey*]から①式を用いて求めた振幅Aを示しており、ほぼ一定値をとることが確認できました。

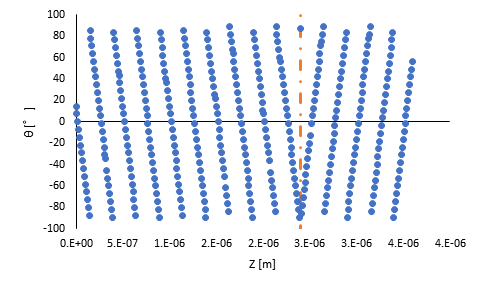
Fig 4は②から求めた位相θを示しており、一定速度で進んでいることが確認できました。
電磁波を複素電磁界で解析することで、電磁波の合成や分離を単純な四則演算で行うことができます。波aと波bで合成された波sumの複素電界を計算してみます。

ここで、

とすると、

となり、単純な足し算で合成波が計算できます。
以下に、ある波と、振幅が同じで位相がΔθだけ遅れた別の波による合成波の複素電界をexpを使って表現してみます。

位相差Δθが定数なので、A{1+exp(iΔθ)}は合成波の振幅になります。この結果をReとImで書き下すと、前述した式が正しいことが分かります。
※電界を複素数ではなく実数値で扱うと、三角関数の公式から考えることになります。

電磁波の合成・分離が、複数の電磁波解析結果の加算・減算で行えることが分かりました。
複素電磁界を用いた電磁波解析結果の加算・減算は以下のページをご参照ください。
加算→https://help.kagiken.co.jp/articles/complex-electromagnetic-field-resultant-wave
減算→https://help.kagiken.co.jp/articles/complex-electromagnetic-field-demultiplexing
減算する際の具体的操作→https://help.kagiken.co.jp/articles/complex-electromagnetic-field-demultiplexing-procedure